Las clases de matemáticas es la que más fracaso escolar generan, es la que más alumnos suspenden y que la que más profesores particulares demanda. Así que si se te está haciendo cuesta arriba, no te preocupes, no estás solo. Te ayudamos a pasar de curso con estos tips para resolver ecuaciones.
Las ecuaciones son sin duda una de partes de esta asignatura que más trabajo cuesta entender. Es a lo que más tiempo se suele dedicar dentro de los años de enseñanza obligatoria. Y es fundamental entenderlo si queremos aprobar matemáticas y seguir con nuestros estudios.
Lo más importante de las ecuaciones es entenderlas y saber reproducir lo que hemos aprendido. Por eso no llevará tiempo dominarlas, no te frustres, intentaremos explicarte como se hace una ecuación de segundo grado, pero siempre puede contratar a un profesor de matemáticas y en pocas horas de clase intensiva las entenderás.
¿Qué son las ecuaciones de segundo grado?
Las ecuaciones son igualdades matemáticas donde desconocemos uno de los términos o números que componen esa igualdad. Y cuando decimos que es de segundo grado significa que ese número desconocido (llamado incógnita) está elevado a potencia dos, es decir, que está multiplicado por sí mismo.
Hay tres tipos de ecuaciones de segundo grado y cada una tiene una forma de realizarla:
- Ecuaciones de segundo grado completas
- Ecuaciones de segundo grado incompletas con ausencia de B
- Ecuaciones de segundo grado incompletas con ausecia de C
¿Pero qué significa la ausencia de B o C? Primero tenemos que entender qué es una ecuación completa y así entenderemos las demás.
¿Cómo se resuelven las ecuaciones de segundo grado completas?
Primero tenemos que entender bien qué son las ecuaciones de segundo grado completas. Todas estas ecuaciones tienen esta estructura:
x2 + x - 2 = 0
Al principio te las encontrarás siempre de esta manera, pero si no lo haces, tendrás que reducirla hasta dejarla de esta manera. Lo primero que tenemos que hacer siempre es dejar todos los valores a un lado para que sea igual a 0.
Después tenemos que aplicar la fórmula para resolver las ecuaciones de segundo grado:
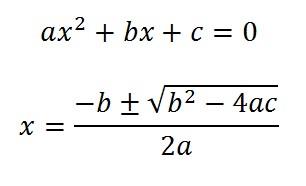
Para no confundir la X con el signo de multiplicaciones esta operaciones la representaremos a partir de ahora con un “ · ”. Pero qué significa a, b y c en esta fórmula. Es muy sencillo:
- La letra a es el valor que acompaña a la x2.
- La letra b es valor que acompaña a la x.
- La letra c es valor que conocemos.
Así que en ejemplo anterior. A sería 1 (si no hay número que acompañe a la x se entiende que es 1), B sería también 1 y C sería en número 2. Y solo tenemos que sustituir estos valores en la fórmula y resolverla como si fuera una ecuación de primer grado.
Si recordamos el orden en el que hay que hacer las operaciones esta es la forma de hacerlo:
- Resolvemos la potencia que está dentro de la raíz cuadrada.
- Resolvemos la suma que está dentro de la raíz cuadrada.
- Resolvemos la raíz cuadrada.
- En este punto puede que te preguntes qué significa que haya un signo + y otro -, esto es porque todas las ecuaciones de segundo grado tiene dos resultados.
- Primer resultado: realizamos la suma y resolvemos la fracción.
- Segundo resultado: realizamos la resta y resolvemos la fracción.
Hay algunas consideraciones que tienes que tener en cuenta para entenderlas al completo:
- Si cuando resolvemos las operaciones dentro de la raíz cuadrada nos da un número negativo es que la ecuación no tiene solución. Porque la raíz cuadrada de un número negativo no existe.
- Si al resolver las operaciones dentro de la raíz da 0, tenemos que poner que es un resultado doble. Ya que sumar o restar este número es indiferente.
Una vez que hayamos entendido y nos salgan bien este tipo de ecuaciones de segundo grado podemos empezar con las incompletas.

¿Cómo resolver ecuaciones de segundo grado incompletas cuando falta B?
Como ya hemos visto antes que nos falte B significa que falta la X que no está elevada a ninguna potencia. Si esta X está pero no tiene ningún valor delante es que tiene el valor 1. Así que esta forma es para cuando solo tenemos la X2 y el valor que conocemos o valor C.
Ejemplo:
x2 - 25 = 0
Como hemos visto en la ecuaciones complejas, si no tenemos esta estructura, tendremos que simplificar la ecuación hasta obtenerla. Después podemos usar la fórmula que hemos visto antes, pero cuando tengamos que poner la B ponemos un 0.
Aprende a resolver ecuaciones con un profe particular
Aunque hay una forma de resolver estas ecuaciones mucho más sencilla:
- Pasamos el valor conocido al otro lado del igual.
Ejemplo: tenemos x2 - 25 = 0 y la dejamos así: x2 = 25
- Pasamo la potencia al otro lado de la ecuación en forma de raíz cuadrada
Ejemplo: x = √ 25
- Resolvemos y el resultado será en positivo y en negativo.
Ejemplo: x = + 5 y x = -5
Tenemos que recordar que si al pasar la potencia nos encontramos con una raíz cuadrada negativa tenemos el resultado no existe. Si x2 tuviera algún tipo de valor pasa al otro lado dividiendo y tendríamos que realizar esta acción ante de pasar la potencia.
¿Cómo resolver ecuaciones de segundo grado incompletas cuando nos falta la C?
Esta es el último tipo de ecuaciones de segundo grado que existe y es simplemente cuando desconocemos todos los valores. Es decir que no tenemos el término C o término conocido y solo tenemos x2 y x en la ecuación.
Lo que tenemos que saber primero es sacar el factor de polinomios, si desconoces este tema, es bueno que lo repases antes de continuar.
Como siempre en estas ecuaciones lo primero que tenemos que hacer es reducirla para dejar una estructura parecida a esta:
x2 - 9x = 0
Después seguimos con los pasos propios para resolver este tipo de ecuaciones:
- Encontramos el factor común que tiene los valores del polinomio:
Ejemplo: en este caso es la x así que dejamos la ecuación así: x ( x - 9) = 0
- El primer resultado es la x fuera del paréntesis que vale 0
- El segundo resultado es la ecuación solo con los valores que están dentro del paréntesis.
Ejemplo: x - 9 = 0
- Solo tenemos que resolver, en este ejemplo el resultado es 9.
Esta es la forma más sencilla de resolver este tipo de ecuaciones, también podemos aplicar la fórmula y sustituir C por 0, pero será mucho más complicado. Aunque cualquier camino es válido si al final llegamos al resultado de la ecuación.
- 10 ejercicios de ecuaciones matemáticas
- ¿Cómo resolver ecuaciones mayores de segundo grado?
- ¿Cómo resolver ecuaciones de segundo grado de la forma más sencilla?
- ¿Cómo hacer ecuaciones de primer grado?
- Cómo resolver paso a paso las ecuaciones matemáticas





